Analyse the continuous beam by moment distribution methods , draw BENDING MOMENT diagram, shear Force and elastic curve ?

1.        Analyse the continuous beam by moment distribution methods , draw BENDING MOMENT diagram, shear Force and elastic curve ?

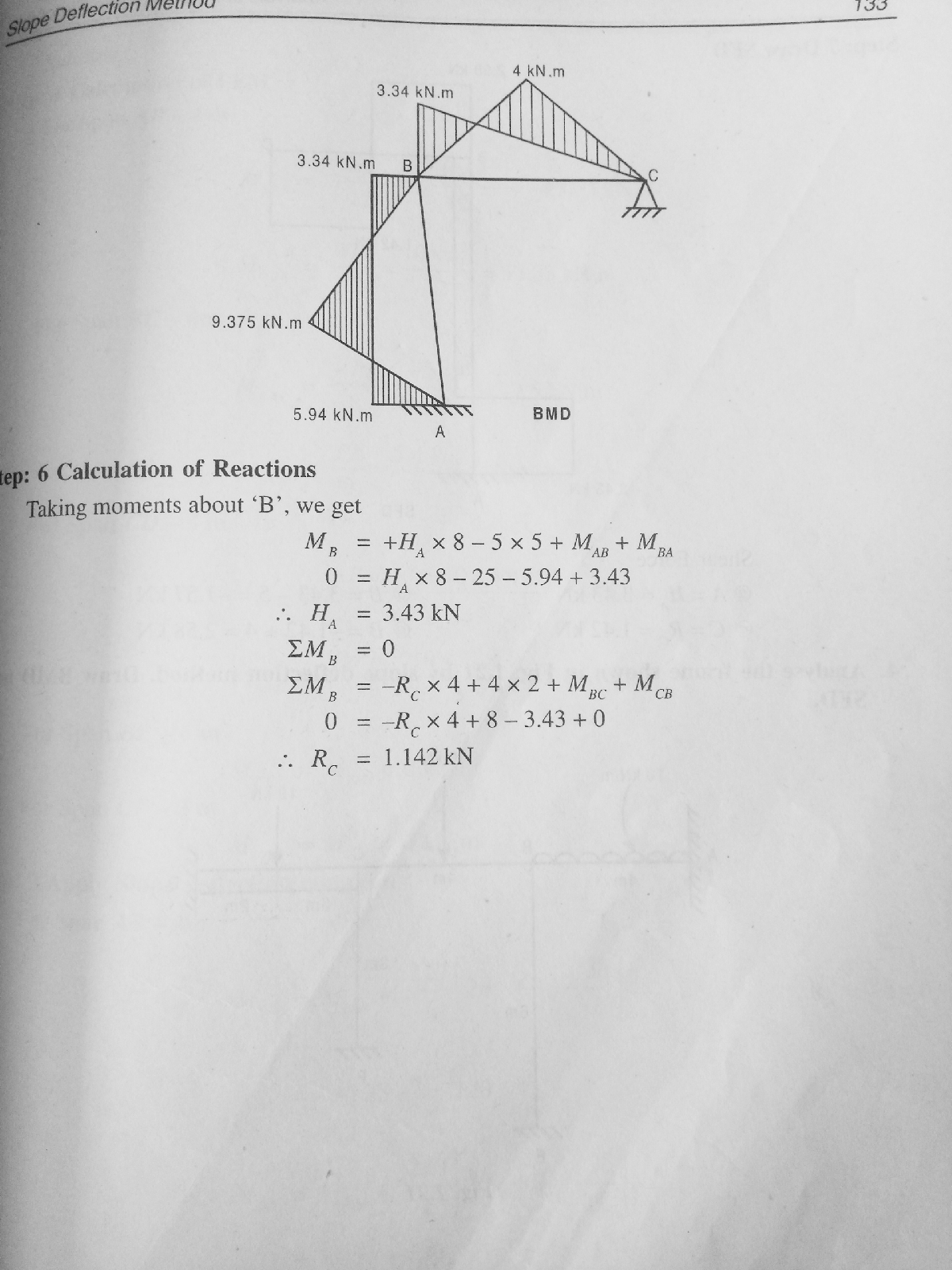
2.Analyse the frame shown in Fig. 2.20 by MDM

    ANALYSIS OF CONTINUOUS BEAMS

Steps

The procedure of analysis by moment distribution method can be explained in the following steps

(a) Determine distribution factors (DF) at each joint, taking into account the modified stiffness

of a member, if far end is hinged or simply supported. Stiffness is zero for the member if far end is free, i.e., overhanging member.

(b) Assume all joints to be locked or restrained against rotation initially. Find out fixed end moments due to loads or settlements for all members.

(C) Release those ends of the members which are actually hinged and carry over its effect to the

far end. Summation of moments in steps (d) and (c) will be initial modified fixed end moments for the moment distribution.

(d) Balance the moments at each joint by releasing the imaginary restraints and distributing the

unbalanced moment to the members at a joint in proportion to the respective distribution

factors.

(e) Take half of the distributed moment to the other end of the member as carry over moment

This will again produce unbalanced moment at the joint.

(f) Balance the joint as shown in (d) and repeat steps (e) and (d) in succession which converges

till the distributed moment becomes negligibly small whose Carry Over (CO) may be neglected.

(g) Sum up the moments to obtain final end moments. We can check that the equilibrium is

satisfied at each joint, 1.e., summation of M =0. (Example M ba, + M bc=0)

Note:

When number of spans are more than two, the distribution and carryover cycles may be

continued up to required accuracy. 1The number of cycles to be carried out is a matter of

practice and judgement. Thus this is an iterative method for analysing structures. Hence.

more the cycles of distribution, less is the error. It 1s suggested that cycle of C.O. may be

stopped when difference in moment are less than So between two consecutive cycles.

Analyse the frame by slope deflection method. Draw BMD SFD ? 2020

1. Analyse the frame shown in below by slope deflection method. Draw deflection

method. Draw BMD and SFD.

2. Analyse the Irane shown in below by slope deflection method. Draw BMD and

SFD.

NOTE:

    Indeterminate Structures/Statically IndeterminateStructures/ Kedundant

Structures

A structure which cannot be analysed with the use of equations of equilibrium or equilibrium

Sometimes it is also called as hyper static structure.

equations only 1s called indeterminate/statically indeterminate/redundant structure.

Along with the basic equilibrium equations, some extra conditions are required to be used

like compatibility conditions of deformations etc., to get the unknown reactions for drawing

bending moment and shear force diagrams.

Examples: Fixed beams, continuous beams, propped cantilever beams, fixed arches, two

hinged arches, multi-storeyed frames etc.

Analyse the continuous beam by slope deflection method and draw BMD, SFD and Elastic curve/slope deflection method//2020

Analysis of indeterminate structure (AIS)

MODULE-1 SLOPE DEFLECTION METHOD

MODULE-2 MOMENT DISTRIBUTION METHOD

MODULE-3 KANI'S METHOD

MODULE -4 MATRIX METHOD OF ANALYSIS (FLEXIBILITY METHOD)

MODULE - 5 MATRIX METHOD OF ANALYSIS (STIFFNESS METHOD)

2. Analyse the continuous beam shown in Fig., by slope deflection method and draw BMD, SFD and Elastic curve

2. alyse the conunous Deam loaded as shown below by slope deflection method.

Take EI is constant tnroughout. Sketch the BMD, SFD and Elastic curve?

visit this link you will get explation in details

https://youtu.be/yhkItRyk26k

what are the Steps in a new highway project work/highway engineering/2020

Steps in a new project work

Ihe various steps in a new highway project may be summarised as given below

(i) Map Study: with the help of available topographic maps of the area.

(i1) ReconnaissanceSurvey: a general idea of a topography and other features, field

1dentification of soils and survey of construction materials, by an on-the-spot inspection of the site.

 

iii) Prelinminary Survey :Topographic details and soil survey along alternate

alignments, consideration of geometric design and other requirements of alignment preparation of plans and comparison of alternate routes; economic analysis and selection of final alignment. Typical plan, longitudinal section and cross section

drawing for the new alignment are shown in Fig. below 

(iv) Location of Final Alignment: Transfer of the alignment from the drawings to the

ground by driving pegs along the centre line of finally chosen alignment; setting

out geometric design elements by location of tangent points, apex points, circular

and transition curves, elevation of centre line and superelevation details.

(v) Detailed Survey :Survey of the highway construction work for the preparation of

longitudinal and cross sections, computations of earth work quantities and other construction material and checking details of geometric design elements.

(vi) Materials Survey: Survey of construction materials, their collection and testing.

(vii) Design: Design details of embankment and cut slopes, foundation of embankments and bridges, and pavement layers.

(vii) Earth Work: Excavations for highway cutting and drainage system, construction of embankments.

(ix) Pavement Construction

Preparation of subgrade, construction of sub-base and Surface courses.

(x) Construction Controls Quality control tests during different stages of

constructions and check for finished road surface such as unevenness, camber,

superelevation and extra widening of pavements at curves.

what are The various factor control the highway alignment/highway engineering/2020

       The various factors which control the highway alignment in general may be listed as

(a) Obligatory points

(b) Traffic

(c) Geometric design

(d) Economics

(e) Other considerations

In hill roads additional care has to be given for :

Stability

Drainage

Geometric standards of hill roads, and

Resisting length

 

(a) Obligatory Points There are control points governing the alignment of the

highways.These control points may be divided broadly into two categories

0 Points through which the alignment is to pass.

(i) Points through which the alignment should not pass.

 Obligatory points through which the road alignment has to pass may cause the

alignment to often deviate from the shortest or easiest path. The various examples of this

category may be bridge site, intermediate town, a mountain pass or a quarry.

When it is necessary to cross hill range. mountains or high ridges the various

alternatives are to cut a tunnel across or to go round the hills or to deviate until a suitable hill pass is available. The suitability of these alternatives depend on many other factors, like the topography and site conditions and cost considerations. the straight alignment

is deviated along the hill side pass, thus avoiding a tunnel or heavy cutting.

(6) Traffic: The alignment should suit trafic requirements. Origin and Destination

study should be carried out in the area and the desire lines be drawn shoWing the trend of traftic flow. The new road to be aligned should keep in view the desired lines, traffic flow patterns and future trends.

(c) Geomeric Design: Geometric design factors such as gradient, radius of curve

and sight distance also would govern the final alignment of the highway. lf straight

alignment is aimed at, often it may be necessary to provide very steep gradients. As tar as possible while aligning a new road, the gradient should be flat and less than the ruling or design gradient. Thus it may be necessary to change the alignment in view of the design speed, maximum allowable superelevation and coefficient of lateral friction. It may be necessary to make adjustment in the horizontal alignment of roads keeping in view the

minimum radius of curve and the transition curves.

     The absolute minimum sight distance, which should invariably be available in every

section of the road, is the safe stopping distance for the fast moving vehicles. Also there

should be enough distance visible ahead for safe overtaking operations of vehicles

speed on the road. Hence the alignment should be finalised in such a moving at design way that the obstructions to visibility do not cause restrictions to the sight distance requirements.

       

(d) Economy: The alignment finalised based on the above factors should also be

economical. In working out the economics, tne initial cost the cost, of maintenance and

vehicle operation should be taken into account. The initial cost of construction can be decreased if high embankments and deep cutings are avoided and the alignment is chosen in a manner to balance the cutting and filling.

(e) Other Considerations: Various other Tactors which may govern the alignment are drainage considerations, hydrological factorS, political considerations and monotony. The vertical alignment is often guided by drainage considerations. The subsurface water level, seepage flow and high flood level are the factors to be kept in view

what are The basic requirements of an ideal highway alignment between two terminal stations/explain briefly/2020

  Requirements

The basic requirements of an ideal alignment between two terminal stations are that it should be

(a) short

 b) easy

(c) safe, and 

 d)economical

     Short It is desirable to have a short (or shortest) alignment between two terminal

stations. A straight alignment would be the shortest, though there may be several

practical considerations which would cause deviations from the shortest path.

    Easy: The alignment should be such that it is easy to construct and maintain the road with minimum problems. Also the alignment should be easy for the operation of vehicles with easy gradients and curves.

     Safe: The alignment should be safe enough for construction and maintenance from the view point of stability of natural hill slopes, embankment and cut slopes and foundation of embankments. Also it should be safe for the traffic operation with safe geometric features.

   Economical: The road alignment could be considered economical only if the total cost including initial cost, maintenance cost and vehicle operation cost is lowest. All these factors should be given due consiaeraton berore Working out the economics of each alignment.

     

     The alignment should be such that 1t would offer maximum utility by serving

maximum population and products. 1he utiity of a road should be judged from its utility value per unit length of road

Briefly explain planning surveys for a highway project?/(VTU 6SEM civil highway engineering) 2020

   PLANNING SURVEYS

Highway planning phase includes

i) Assessment of road length requirement for an area (it may be a district, State r the

whole country)

(ii) Preparation of master plan showing the phasing of plan in annual and or five year

plans.

         Thus for assessing the road length requirement, field surveys are to be carried out to collect the data required for determining the length of the road system. The field surveys thus required for collecting the factual data may be called as planning surveys or Jact jinding surveys. The planning based on the factual data may be considered scientific and

sound.

   The factual studies point to an intelligent approach for planning and these studies  should be carried out if the highway programme is to be protected from inconsistent and short sighted policies.

The planning surveys consist of the following studies; the details shown in Fig. 

(a) Economic studies

(b) Financial studies

(c) Traffic or road use studies

(d) Engineering studies

(a) Economie Studies

The various details to be collected are useful in estimating the economics involved in

the highway development programme. Hence it is desirable to find the service given Dy

each road system to the population and products of the area. All details of the exIsting

facilities should be available before estimating the requirement such that economic

justification can be made for each plan. The details to be collected include the following

(i) Population and its distribution in each village, town or other locality with the area

classified in groups.

(ii) Trend of population growth.

(iii) Agricultural and industrial products and their listing in classified groups, area wise.

(iv) Industrial and agricultural development and future trends.

(v) Existing facilities with regard to communication, recreation and education etc.

(vi) Per capita income.

(b) Financial Studies

The financial studies are essential to study the various financial aspects like sources of income and the manner in which funds for the project may be mobilized. The details to be collected include:

) Sources of income and estimated revenue from taxation on road tranpo

(1i) Living standards

(111) Resources at local level, toll taxes, vehicle registration and fines.

(iv) Future trends in financial aspects.

(c) Traffic or Road Use Studies

All the details of the existing traffic, their volume and pattern of flow should be known Derore any improvement could be planned. Traffic surveys should be carried out in tne wOC area and on selected routes and locations in order to collect the 1olowing particulars

i) trattic volume in vehicles per day, annual average daily traffic, peak and design

hourly traffic volume.

ii) Origin and destination studies

iii) Traffic flow patterns

(iv) Mass transportation facilities

(V) Accidents, their cost analysis and causes

(V1) Future trend and growth in traffic volume and goods traffic; trend in traftic pattern

(vii) Growth of passenger trips and the trend in the choice of modes.

(d) Engineering Studies

All details of the topography, soil and other problems such as drainage, construction

and maintenance problems should be investigated betore a scientific plan or programme is

suggested. The studies include:

(i) Topographic surveys

ii) Soil surveys

(ii) Location and classification of existing roads

(iv) Estimation of possible developments in all aspects due to the proposed highway

development.

(v) Road life studies

(V1) Traffic-studies-Origin and Destination studies

(Vin) Special problems in drainage, construction and maintenance of roads.

Thus all the above studies for collecting the 1actual data for highway planning are

known as fact finding surveys. The details collected are tabulated and plotted on th

maps of the area under planning